Electron transfer theory

Electron / hole transfer process on electrode
In general the electrolyte can be a reducing agent: solution injecting electron to the electrode, and oxidising agent: solution extracting electron from the electrode. Also holes can be captured instead of electron injection or holes can be injected instead of extracting electron as this two charge carrier interchangeable in electrochemical processes (Morrison 1980).

For example the two following reaction are equal:
e- + Ag —> Ag or Ag+ —> Ag + h+

Marcus model of electron transfer
Marcus introduced the electron transfer model in 1956. He received the Nobel prize for this theory in 1992. Currently this is the dominant quantum physics-based semi classical electron transfer model, although in the last decade the fully quantum physics-based theory was created.

The theory is based on the Franck-Condon principle, which states that at the moment of the electron transfer no electron structure adjustment is possible because the reaction time is many magnitudes smaller than the time necessary for structural adjustment. This was combined with the previously known chemical reaction energy barrier.

Marcus found that in many cases of electron transfer, the theoretical energy barrier would be too high for the reaction to occur with the experimental rate. If the energy states are fluctuating, the pre electron transfer and post electron transfer can have the same energy level. In this case the energy barrier is the lowest for the reaction.

The theory proceeded as follows:

“The potential energy of the entire system, reactants plus solvents, is a function of the many thousands of relevant coordinates of the system. These coordinates include position and orientation of individual solvent molecules and vibration coordinates of reactants.”
(Marcus 1993)

The energy potential of reactants and products is illustrated in Figure 1.1. Electron transfer can occur when the potential of the reactant crosses the potential of product. In this case in an electron available the electron jump will happen and the product continues to move on its corresponding potential curve.

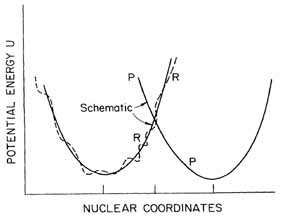
Figure 1.1 Potential surface of reactants and products R curve illustrates the reactants plus environment, P curve is the products and environment. Abscissa is a multidimensional space, includes thousands of coordinates.

In the case of when the energy splitting in not enough to reach the curve’s intersection point, the probability of the interaction can be calculated with quantum mechanical methods, like the Fermi golden rule (Landau-Zener extended to multi dimension use).

Marcus theory provides an electron transfer rate calculation based on electron coupling and activation energy. Activation energy is based on the reorganisation energy and Gibbs free energy.

shows the redox process on the C- side of the semiconductor, (i) redox couple can extract electron from the semiconductor, this cause the reduction of the ion. (ii) redox couple can inject hole to the electrode, in this way the ion reduction will occur shows the redox process on the C+ side of the semiconductor (iii) redox couple can inject electron to the electrode, and in this way it oxidise itself. (iv) redox couple can extract hole from the electrode and it can be reduced Usually valance band process can be anticipated on the C-, because the positive polarity ions can be attached to the surface, and negative ions pushed away. Similarly, based on this model, valance band process can be easier to accommodate with negatively charged ions.

In the case of potential applied electrochemical reaction, the potential translates the free energy curve to the reduced energy barrier position.

Since its creation the Marcus electron transfer theory had a number of modifications in the way of calculating the factors, but the base of the theory remained as described above.

Electron transfer in semiconductors
When a semiconductor is in contact with an electrolyte, its Fermi level is equal with the dominant redox potential of the electrolyte when the system is in equilibrium. In the case of there being no current flowing, there is no net electron transfer.

In semiconductor electron transfer the most dominate factors are the Fermi distribution of electron in the solid and the fluctuation of energy levels in ions. In only these factors are included in the model. If all other factors are neglected, electron transfer occurs when the energy level of the ion fluctuates to the same level as the conduction or valance band. At this point electron transfer can happen with minimal change in electron energy. The electron transfer rate is proportional to the number of ions available on the surface, the number of charge carriers on the surface and the probability that the energy level of the ion fluctuates to the appropriate state (Figure 1.).

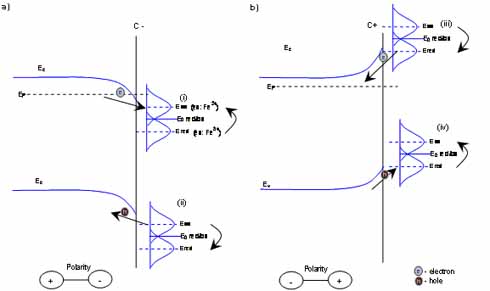
Figure 1.3 Charge transfer on semiconductor-electrolyte interface shows the redox process on the C- side of the semiconductor, (i) redox couple can extract electron from the semiconductor, this cause the reduction of the ion. (ii) redox couple can inject hole to the electrode, in this way the ion reduction will occur shows the redox process on the C+ side of the semiconductor (iii) redox couple can inject electron to the electrode, and in this way it oxidise itself. (iv) redox couple can extract hole from the electrode and it can be reduced Usually valance band process can be anticipated on the C-, because the positive polarity ions can be attached to the surface, and negative ions pushed away. Similarly, based on this model, valance band process can be easier to accommodate with negatively charged ions.

Charge transfer can also occur on surface states. This factor is widening the range of the possible redox processed on the surface.

If the electrode – electrolyte energy levels are not match (and there is no appropriate surface state), the energy transfer still can occur with tunneling mechanism (furthermore ions on the surface can act as bridge for tunneling). For tunneling the ions need to be no more than a certain distance (usually less than 40 Angstrom) from the surface (Figure 1.).

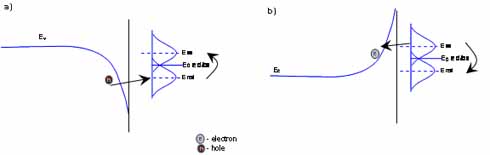
Figure 1.4 Tunneling process in valance and conduction band Tunneling in valance band: the fluctuation of the reduced ion is too high for direct valance band electron transfer. The tunneling mechanism can make the redox process possible. Electron tunneling in conduction band Tunneling is also possible if positive ion transfer charge on the positively poled surface of a semiconductor.

References
Marcus, R. A. (1993) ‘ELECTRON-TRANSFER REACTIONS IN CHEMISTRY – THEORY AND EXPERIMENT (NOBEL LECTURE)’, Angewandte Chemie-International Edition in English, 32(8), 1111-1121.

Morrison, S. R. (1980) Electrochemistry at semiconductor and oxidized metal electrodes, New York ; London: Plenum.