Essay on Mathematical Modelling

Q- Write a formal academic essay which critically analyses the potential of mathematical modelling to enrich and enhance pupils’ mathematical experiences

Berry et al. (1984) define mathematical modelling as being the process of an individual applying their numerical skills to a real-life problem or situation. Mooney and Swift (1999) construe it more precisely as being a representation of reality with a purpose, i.e. to solve an issue. Rowlands (2008, p.196) argues that the majority of mathematical models are mechanical although Koshy and Murray (2011) argue that modelling is a holistic process which can be applied to a plethora of mathematical situations. Regardless of the exact definition of modelling, it seems to be more prevalent in the mathematics curriculum under recent government reforms. DfE (2013) articulate the importance of pupils becoming fluent in mathematics by following a line of enquiry and developing an argument, which modelling could be a tool for developing such understanding.

Denscombe (2010) argues that modelling in any context has the duality of helping a child develop both inductive (observing and formulating a model and relating it to theory) and deductive (applying a theoretical model to their investigation) thinking. Conversely, Piaget (1952; 1953) argues that children are not capable of thinking deductively until they are 14, which makes any deductive teaching strategies before this age ineffective. Johnston- Wilder (2005; 2011) claims that this potential lack of understanding can be offset by careful facilitation of the teacher, particularly by using ICT and other technological innovations. Bruner (1966) validates this by theorising that any a child of any age can learn a task, provided they have been given the right instruction and support. Ultimately, Askew et al. (1997) reason that the success of any mathematical teaching approach depends on the mind set and orientation of the teacher, particularly as Gregorc (1986) demonstrates that practitioners normally teach in their preferred modality of learning.

The orientation of the teacher could really impact on the success of the modelling in developing children’s understanding. Bruner (1961, p.20) conjectures that, if modelling was taught in a constructive manner, where the learner discovers things for themselves, then it will be even more potent. Dale (1970) reaffirms this in his cone of learning, by stating that children learn 90% of ‘what they do.’

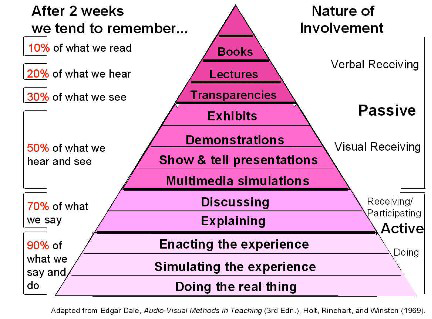
Cone of Learning

(Dale, 1970)

Expanding on this, Watson and Mason (2005) hypothesise that this style of teaching could have an even greater effect if learners are given a degree of trust in the lesson, such as generating their own examples. However, Pimm (1988) advises teachers to exercise caution on this approach, as to little guidance and involvement from the teacher could result in the pupils not staying within the parameters of the investigation. It could be surmised that the guided discovery teaching style advocated by Mosston and Ashworth (2002) where the teacher and learner both have roughly equal involvement in the learning process, is one of the more effective ways of teaching modelling. Berry et al. (1984) collaborate with this viewpoint by identifying a mixture of interactive, whole class and discovery teaching styles as being conducive to teaching mathematical modelling.

Krathwohl (2002, p.214) suggests that modelling could be a useful metacognitive activity, as it gets pupils to think about what they are learning, by analysing and adapting their methods and synthesising new methods. Savage (2011) couches this in a slightly different manner by identifying the potential of modelling to be a tool for developing rich cross-curricular links, particularly with Science (a lot of mathematical models are related to science) and English (when undertaking modelling pupils communicate with each other and should write their investigation up in a clear and coherent manner). DfE and Ofsted (2012) recognise that mathematics is a universal language, and that its links with English need to be made explicit in lessons. Sperry (1961, p.1750) suggests that combining subjects at the opposite ends of the left-right brain continuum will result in a process of lateralisation, where a person learns in the optimum manner by utilising both hemispheres of their brain simultaneously. Gardner (2004) is a proponent of teachers recognising pupils’ different learning styles, and modelling could be a tool in which to do so, although it may be impractical to consider the learning style of every child in the class. Additionally, Biggs (1999) argues that an activity like modelling does not fairly disseminate active and passive learning, and that those pupils who do not learn in a kinaesthetic manner may be neglected when doing modelling. Conversely, from his ethnographic study of machine workers, Orr (1996) concluded that people will learn in an environment that is relevant to them. Lave and Wenger (1991) term this as ‘situated learning’ and the abundant real-life applications of modelling may mean that pupils will learn in some manner, whether they have a passive or active orientation.

Biggs (2003) makes the valid point that, although modelling is a multi-faceted activity with pedagogical richness, it should still be aligned to the curriculum in some manner, preferably through a triangle of assessment, teaching style and lesson objectives:

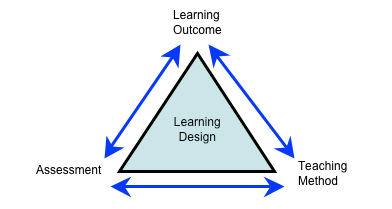
Whilst recognising the need for a national curriculum, Chambers (2008) advocates flexibility in mathematics teaching, to help the learners develop as much as possible. Bartlett (2013) agrees with this, as she states that some of the best mathematics lessons she has taught, in terms of both the progression and enjoyment of the pupils, have been spontaneous and flexible. Nevertheless, Hansen (2011) identifies the need for a quorum of planning in mathematical activities, to avoid errors and misconceptions. This contrast starkly with a constructivist approach to teaching, were errors and misconceptions are promoted as a tool of discovery and understanding for the pupils. Mason et al. (2010) identify that a degree of planning in mathematical modelling will result in an activity that is commensurate with the abilities of the pupils where appropriate differentiation can be made. Regardless of the various assimilation of the pedagogical viewpoints concerning modelling, it could be argued that the most important factors that decides how modelling is taught are the topic it covers and the ability and behaviour of the class being taught it.

In conclusion, modelling could be a very useful tool for promoting mathematical understanding, if it is used carefully and in the appropriate manner.

References

Askew, M., Brown, M., Rhodes, V., Wiliam, D. and Johnson, D. (1997) Effective Teachers of Numeracy in Primary Schools: Teachers’ Beliefs, Practices and Pupils’ Learning. York: British Educational Research Association.

Ashworth, S. (2002) Teaching Physical Education. 5th edn. San Francisco: Benjamin Cummings.

Bartlett, J. (2013) Becoming an Outstanding Mathematics Teacher. London: Routledge.

Berry, S, J., Burghes, N, D., Huntley, I, D., James, J, D. and Moscardini, A. (1984) Teaching and Applying Mathematical Modelling. Chichester: Ellis Horwood.

Biggs, J. (1999) Teaching for Quality Learning at University. Buckingham: Open University Press.

Bruner, J. S. (1961) ‘The act of discovery.’ Harvard Educational Review, 31, pp. 21-32.

Bruner, J. S. (1966) Toward a Theory of Instruction. Cambridge, Mass.: Belkapp Press.

Chambers, P. (2008) Teaching Mathematics. London: Sage Publications.

Dale, E. (1970) ‘Dale’s cone of Learning.’ Theory into Practice, 9 (2).

Denscombe, M. (2010) The Good Research Guide: for small-scale research projects. London: Oxford University Press.

Gardner, H. (2004) Changing Minds: The art and science of changing our own and other people’s minds. New York: Harvard Business School Press.

Great Britain. Department for Education (2012) The Standards for meeting Qualified Teacher Status. London: DfE.

Great Britain. Department for Education (2013) The mathematics National Curriculum in England. Framework document for July 2013- for delivery from September 2014. London: DfE.

Great Britain. Ofsted (2012) Mathematics made to Measure. London: Ofsted.

Gregorc, A. (1986) Gregorc Style Delineator: Development, Technical, and Administration Manual. Gregorc Associates, Inc.

Hanson, A. (2011) Children’s errors in mathematics: understanding common misconception in primary schools. 2nd edn. Exeter: Learning Matters.

Johnston-Wilder, S. (2005) Teaching Secondary Mathematics with ICT. London: Open University Press.

Johnston-Wilder, S. (2011) Learning to Teach Mathematics in the Secondary School. 3^rd London: Routledge.

Koshy, V. and Murray, J. (2011) Unlocking Mathematics Teaching. London: Taylor and Francis.

Krathwohl, D. R. (2002) ‘A revision of bloom’s taxonomy: An overview.’ Theory into Practice, 41 (4): pp. 212-218.

Lave, J. and Wenger, E. (1991) Situated Learning: Legitimate Peripheral Participation. Cambridge: Cambridge University Press.

Mason, J. and Watson, A. (2005) Mathematics as a constructive activity; learners generating examples. Mahwah: Lawrence Erlbaum Associates.

Mason, J., Burton, L. and Stacey, K. (2010) Thinking Mathematically. London: Prentice Hall.

Mooney, D. and Swift, R, J. (1999) A course in mathematical modelling. Washington: Mathematical Association of America.

Orr, J, E. (1996) Talking about Machines: Ethnography of a Modern Job. New York: ILR Press.

Piaget, J. (1952) The Origins of Intelligence in Children. New York: International University Press.

Piaget, J. (1953) The Origins of Intelligence in Children. London: Routledge and Kegan Paul.

Pimm, D. (1988) Mathematics, teachers and children: a reader. London: Hodder and Stoughton.

Rowlands, S. (2008) ‘Why mechanics should be integral to secondary school mathematics.’ Teaching Mathematics and its Applications. 27 (4), pp. 187-199.

Savage, J. (2011) Cross-Curricular learning and teaching in the Secondary school. London: Routledge.

Sperry, R. W. (1961) ‘Cerebral Organization and Behavior: The split brain behaves in many respects like two separate brains, providing new research possibilities.’ Science 133 (3466): pp. 1749–1757.